옵티마이저(Optimizer)
옵티마이저는 경사를 내려가는 방법을 결정

일반적인 경사 하강법(GD)에서는 모든 입력 데이터에 대한 손실 함수의 기울기를 계산한 후 가중치 업데이트
즉, Iteration 마다 모든 데이터를 다 사용
입력 데이터가 적다면 이 방법으로도 빠르게 가중치 갱신 가능
실제로는 큰 데이터를 다루기 때문에 모든 데이터에 대해 손실을 계산하는 과정이 굉장히 오레 걸림
확률적 경사 하강법(Stochastic Gradient Descent, SGD)
전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산
그 손실 정보를 역전파하여 신경망의 가중치를 업데이트
Iteration 마다 1개의 데이터만 사용
가중치를 빠르게 업데이트 할 수 있다는 장점
1개의 데이터만 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다는 단점


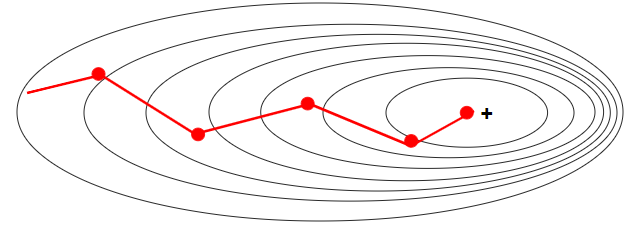
위의 그림에서 확률적 경사 하강법과 일반적인 경사 하가업에서 경사 하강이 어떻게 일어나는지 차이를 볼 수 있음
이 두 방법을 적절히 융화한 미니 배치 (Mini-bagch) 경사 하강법이 당장
N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치 업데이트
즉, Iteration 마다 N(= 배치 사이즈)개 데이터 사용
일반적으로 두 방법의 장점을 적절히 융화한 미니 배치 경사 하강법을 많이 사용
- 배치 사이즈 (Batch Size)
미니 배치 경사 하강법에서 사용하는 미니 배치의 크기
일반적으로 배치 사이즈는 2의 배수로 설정하며, 메모리 크기가 허락한다면 큰 배치 사이즈를 쓰는 것이 학습을 안정적으로 진행할 수 있음 - # of Data, Epoch, 배치 사잊, iteration 관계
Epcohs는 데이터셋 전체를 몇 번이나 반복하여 학습할 지를 결정
Iteration은 순전파-역전파 1회, 즉 가중치를 한 번 수정하는 단위
따라서 데이터셋을 이루는 데이터의 수, 배치 사이즈, Iteration 식은
# of Data = Batch_size X Iteration
여러가지 옵티마이저 중에서 어떤 것이 가장 좋다고 말하기는 어려움
문제마다, 데이터마다 달라지기 때문에 여러 옵티마이저를 적용하면서 서로 비교
최적의 하이퍼파라미터를 찾아보면서 여러 옵티마이저 비교