RIMI CODE

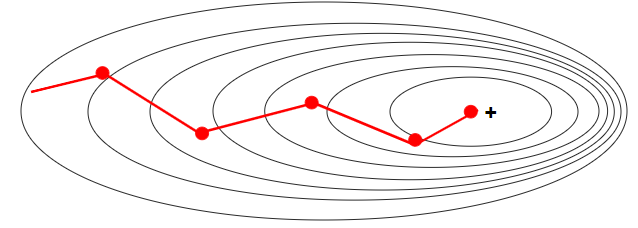
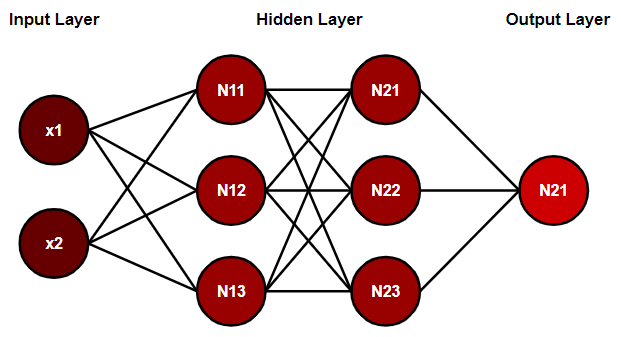
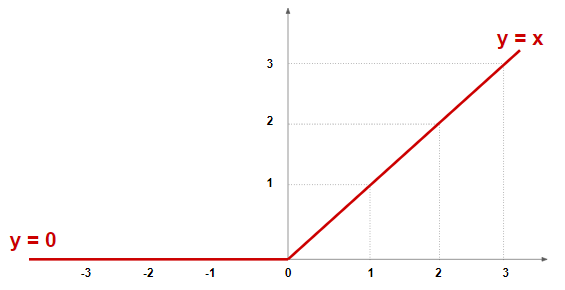
배치 사이즈는 주로 2의 제곱수 배치 사이즈가 작을 때 배치 사이즈를 너무 작게 설정하면 경사 하강법을 통한 가중치 갱신이 불안정하여 최적점에 이르기까지 많은 Iteration을 필요로 한다는 단점 하지만 노이즈가 상대적으로 높기 때문에 지역 최적점(Local Minima)에 빠져나올 확률이 높아진다는 장점 배치 사이즈가 클 때 경사 하강법 과정에서 가중치 갱신이 안정적으로 일어나기 때문에 학습 속도가 빨라짐 배치 사이즈가 1인 확률적 경사 하강법보다 미니 배치 사용한 미니 배치 경사 하강법이 더 빠르게 수렴 큰 배치 사이즈가 좋다고 배치 사이즈를 너무 크게 설정하면 메모리를 초과해버리는 Out-of-Memory 문제 발생 최적의 배치 사이즈 배치 사이즈가 클 때 학습이 안정적으로 잘 되는 것은 사실이지..

옵티마이저는 경사를 내려가는 방법을 결정 일반적인 경사 하강법(GD)에서는 모든 입력 데이터에 대한 손실 함수의 기울기를 계산한 후 가중치 업데이트 즉, Iteration 마다 모든 데이터를 다 사용 입력 데이터가 적다면 이 방법으로도 빠르게 가중치 갱신 가능 실제로는 큰 데이터를 다루기 때문에 모든 데이터에 대해 손실을 계산하는 과정이 굉장히 오레 걸림 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 전체 데이터에서 하나의 데이터를 뽑아서 신경망에 입력한 후 손실을 계산 그 손실 정보를 역전파하여 신경망의 가중치를 업데이트 Iteration 마다 1개의 데이터만 사용 가중치를 빠르게 업데이트 할 수 있다는 장점 1개의 데이터만 보기 때문에 학습 과정에서 불안정한 경사 하..

손실 함수 J 의 경사(Gradient)가 작아지는 방향으로 업데이트 하면 손실 함수의 값을 줄일 수 있음 매 Iteration 마다 해당 가중치에서의 비용 함수의 도함수(=비용 함수를 미분한 함수)를 계산하여 경사가 작아질 수 있도록 가중치 변경 기울기 반대 방향으로 배 만큼 이동 각각의 가중치는 역전파의 주요 메커니즘인 편미분과 Chain Rule(연쇄 법칙)이 사용 특정 가중치에 대한 기울기는 손실 함수를 해당 가중치로 편미분 모든 가중치에 대한 값은 Chain Rule로 구함 연쇄 법칙이란 특정 변수에 대한 (편)미분 값을 다른 변수의 미분을 사용하여 나타낼 수 있는 방식 연쇄 법칙을 사용하여 각 변수가 얼마나 수정되어야 할 지에 대한 정보를 전달

신경망 학습 진행 과정 1. 데이터가 입력되면 신경망 각 층에서 가중치 및 활성화 함수 연산을 반복적으로 수행 2. 1의 과정을 모든 층에서 반복한 후에 출력층에서 계산된 값을 출력 3. 손실 함수를 사용하여 예측값(Prediction)과 실제값(Target)의 차이 계산 4. 경사하강법과 역전파를 통해서 각 가중치를 갱신 5. 학습 중지 기준을 만족할 때까지 1~4의 과정을 반복 1 ~ 4 과정을 Iteration(이터레이션) 이라고 하며 매 Iteration 마다 가중치가 갱신 순전파, 손실 계산, 역전파로 나누어짐 - 순전파: 예측하기 - 손실 함수: 실제 값과의 차이 계산 - 역전파: 가중치 수정 순전파(Forward Propagation) 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서..

기울기 소실(Vanishing Gradient or Gradient Vanishing) 활성화 함수의 미분값이 0에 가까워져 학습이 잘 되지 않는 현상 시그모이드 함수를 활성화 함수로 하는 은닉층을 깊게 쌓았을 때 기울기 소실 문제 발생 시그모이드 함수의 도함수 미분값 < 1 때문에 신경망을 학습하는 과정에서 시그모이드 미분값이 곱해지게 되면 갱신되어야 하는 값이 작아져 학습이 제대로 이루어지지 않음 ReLU 함수 ReLU 함수는 음수 구간에서는 미분값이 0 이지만, 양수 구간에서는 미분값이 1 층이 깊어지더라도 1의 값이 계속 곱해지기 때문에 기울기 값이 과도하게 커지거나 작아지는 문제 발생하지 않음 ReLU 함수 등장 이전까지는 은닉층을 깊게 쌓을 수 없었기 때문에 복잡한 문제 푸는데 딥러닝을 사용할..

모든 활성화 함수의 공통점은 비선형(Non-linear)이라는 점 활성화 함수가 선형이면 안되는 이유 예를 들어, 선형인 활성화 함수 l(x) = ax + b 가 있다고 가정 이 함수를 사용하여 3개의 층을 쌓는다면 최종적인 활성화 함수는 이 때, 라고 하면, 로 여전히 같은 형태의 함수를 사용 즉, 층을 아무리 깊게 쌓아도 여러 층을 쌓는 이점을 살리지 못하게 됨 여러 층을 쌓을 때의 장점을 살리기 위해 비선형 함수 사용

가중치 행렬 신경망에서 실제로 학습되는 부분은 각 가중치 위 그림에서 화살표 하나마다 각각의 가중치가 주어짐 입력층에 3개의 노드, 은닉층에 4개의 노드 두 층 사이에 12개의 가중치 존재 가중치가 연산되는 과정을 컴퓨터에서 잘 연산하기 위해 행렬의 형태로 만들어 주어야 함 행렬의 Shape 퍼셉트론에 있는 가중치-편향 연산은 행렬 곱으로 연산 행렬곱 연산을 잘 수행하려면 각각의 Shape을 잘 수행해야 함 y = Wx 위 수식에서 가중치 행렬을 W, 입력 벡터를 x 라고 하면 연산의 결과로 출력되는 벡터는 y 입력 벡터의 형태에 따라 가중치 행렬의 Shape 이 결정 Keras 로 구축한 신경망에서 가중치 행렬의 Shape Keras 에서는 은닉층 및 출력층의 노드 수만 설정해주면 자동으로 가중치 행렬..

인공 신경망 딥러닝(Deep Learning)은 인공 신경망의 층을 깊게(Deep) 쌓은 것 ANN(Artificial Neural Networks), 즉 인공 신경망은 실제 신경계를 모사하여 만들어진 계산 모델 줄여서 뉴럴넷(Neural-Net)으로 부르기도 함 퍼셉트론을 다층으로 쌓는 이유 1개의 분류기로는 XOR GATE 문제를 풀 수 있음 1개의 층으로는 해결할 수 없던 문제도 2개 이상의 층으로 구성하면 풀 수 있음 퍼셉트론을 여러 개의 층으로 쌓아 구축한 신경망 => 다층 퍼셉트론 신경망(Multi-Layer Perceptron, MLP)라고 함 입력층(Input Layer) 데이터셋이 입력되는 층 입력되는 데이터셋의 특성(Feature)에 따라 입력층 노드의 수가 결정 보통 어떤 계산도 수행..

퍼셉트론의 가장 단순한 형태는 AND, NAND, OR과 같은 논리 게이트(Logic Gate) AND GATE 입력 신호가 모두 1일 때 1을 출력 즉, 두 조건을 만족할 때만 동작 NAND GATE Not AND 의 줄임말로 AND GATE 결과의 반대를 출력 OR GATE 입력 신호 중 하나만 1이라도 1을 출력 XOR GATE 배타적 논리합(Exclusive-OR)이라고도 불리는 GATE 입력 신호가 다를 경우 1을 출력 신경망이 논의되던 초기에 퍼셉트론의 한계로 지적되었던 것 Linear separability 위 그래프는 각각 AND, OR, XOR의 진리표를 나타내고 있는 그림 검은색이 1, 흰색이 0을 나타냄 AND와 OR에 해당하는 그래프에는 두 클래스를 분류하기 위한 분류 경계 XOR에..

계단 함수 (Step function) 가장 간단한 활성화 함수 입력값이 임계값을 넘기면 1을 그렇지 않으면 0을 출력하는 함수 임계값 지점에서 미분이 불가능하고 나머지 지점에서는 미분값이 0이 나옴 실제로 계단 함수를 활성화 함수로 사용하면 학습이 제대로 이루어지지 않음 시그모이드 함수 (Sigmoid function) 신경망이 경사 하강법을 통해 학습을 진행하기 위해서는 미분 과정이 필요 계단 함수의 단점을 해결하기 위해 사용된 함수 임계값보다 작은 부분은 0에 가까워지고, 큰 부분은 1에 가까워짐 계단 함수보다 부드럽게 연결되어 있기 때문에 모든 지점에서 미분이 가능하며, 미분값도 0이 아님 중복 사용하게 되면 기울기 소실(Vanishing Gradient) 문제 발생 ReLU 함수 (ReLU fu..